Introduction

Consider reading an article on Wikipedia. You read until you encounter an unfamiliar term, then you click it to open a new article. You continue this process until you have several pages open simultaneously. Then you receive a phone call. It is a close friend, and you choose to derail your studies for a few minutes. After your chat, you return to your browser and try to pick up where you left off. You find a series of tabs open. The tab farthest to the left was your original article. The tab farthest to the right was the most recent. The tabs between occur in the order in which you clicked related articles.

You decide you must be as systematic as possible as you get back to your train of thought. Should you start at the leftmost or rightmost tab? What can we determine about these options?

• Left-to-right: In this strategy, you choose to go back to reading the original article you opened. After all, it was the most important when you sat down to start your research, so you should probably get started there. Then as needed, you can continue to work through other tabs. If you choose this strategy, it is because you assume that you had opened tabs because you might be interested in them later.
• Right-to-left: In this strategy, you assume that you opened “Formal system” because you wanted to understand it better while reading “Decidability (logic),” which was open because you were reading “Decision problem.” If you choose this strategy, it is because you assume that you opened each additional tab due to some context present in the prior tab.

Both strategies share some commonalities. New information was encountered in some sort of linear fashion. The choice is which to prioritize. Is it important to process the information in the order it was received? Or is it more important to process the most recent information first? Here we have a problem with two reasonable solutions depending on our original expectations and desired outcome.

These options reflect two related but distinct abstractions. Both queues and stacks store values in a sequential manner in the order in which they arrived. A queue processes the input that arrived first before that which arrived second. For this reason, we consider queues to have a first-in-first-out (or FIFO) property. A stack instead processes the most recently received input first. Likewise, we consider stacks to have a last-in-first-out (or LIFO) property.

Queues are always present in our natural life. Whenever we “line up” for something, we have formed a queue. Queues have a visceral fairness about them. Those who arrived at the grocery store checkout first are served first. Those in line earlier for that big movie premiere are more likely to get seats. Queues are also convenient because they preserve a temporal sequence. Consider a system like a document editor. You specify changes to the document, and those changes are made. These must be processed in the order they are received because one change is likely dependent on whether the prior has been completed.

However, queues are not always the most expressive way to process a stream of data. Consider the call stack from our prior investigation of recursion in chapter 2. Each new function call encountered is processed within the context of the function call that came prior. While it is true that some other function call came before that, we are more concerned with maintaining the contextual reference rather than the temporal one. Stacks are also convenient when no implied order or precedence is required. In that case, inserting and retrieving data from the same end of the structure (LIFO) is often more efficient than the FIFO alternative.

You may have noticed that we have not explicitly referred to stacks and queues as data structures. While the term “data structure” may be considered appropriate for queues and stacks, a more appropriate description would be abstract data type. This distinction will be the first topic of this chapter.

Abstract Data Types

With linked lists, we described desired operations alongside a specific structure that satisfies that behavior. At times it is beneficial to decouple the two. The nodes represented the data structure, while the set of desired operations (such as insertion and deletion) formed what is called the abstract data type (ADT).

In this chapter, we define queues and stacks as abstract data types before specifying underlying data structures. Different reference texts specify slightly different operations. For the purposes of this text, we define queue and stack with three defined operations:

Queue

• enqueue: places an element at the tail of the queue
• dequeue: removes the next available element from the head of the queue
• isEmpty: returns true or false depending on whether the underlying data structure has any remaining elements

Stack

• push: places an element at the top of a stack
• pop: removes an element from the top of a stack
• isEmpty: returns true or false depending on whether the underlying data structure has any remaining elements

We have three important nuances thus far:

1. We have not specified exactly how we intend to guarantee these operations or how we will store elements until we dequeue or pop them.
2. The above definitions use words like head, tail, and top. From one text to another, these words may change. The important part is that queues have elements entering on one end and leaving from the other. Stacks have elements entering and leaving from the same orientation.
3. We cannot yet specify the runtime of any of these operations. We can only do so once the actual underlying data structures have been specified.

In the following sections, we illustrate how these operations can be satisfied with linked lists or arrays.

Linked Lists

Linked lists are well suited for both queues and stacks. First, adding and removing elements is simply a matter of creating a node and setting a reference or removing a reference. Second, we have a fairly intuitive means of tracking both ends of the data structure. For purposes of this section, we will assume a singly linked node discussed earlier in this book.

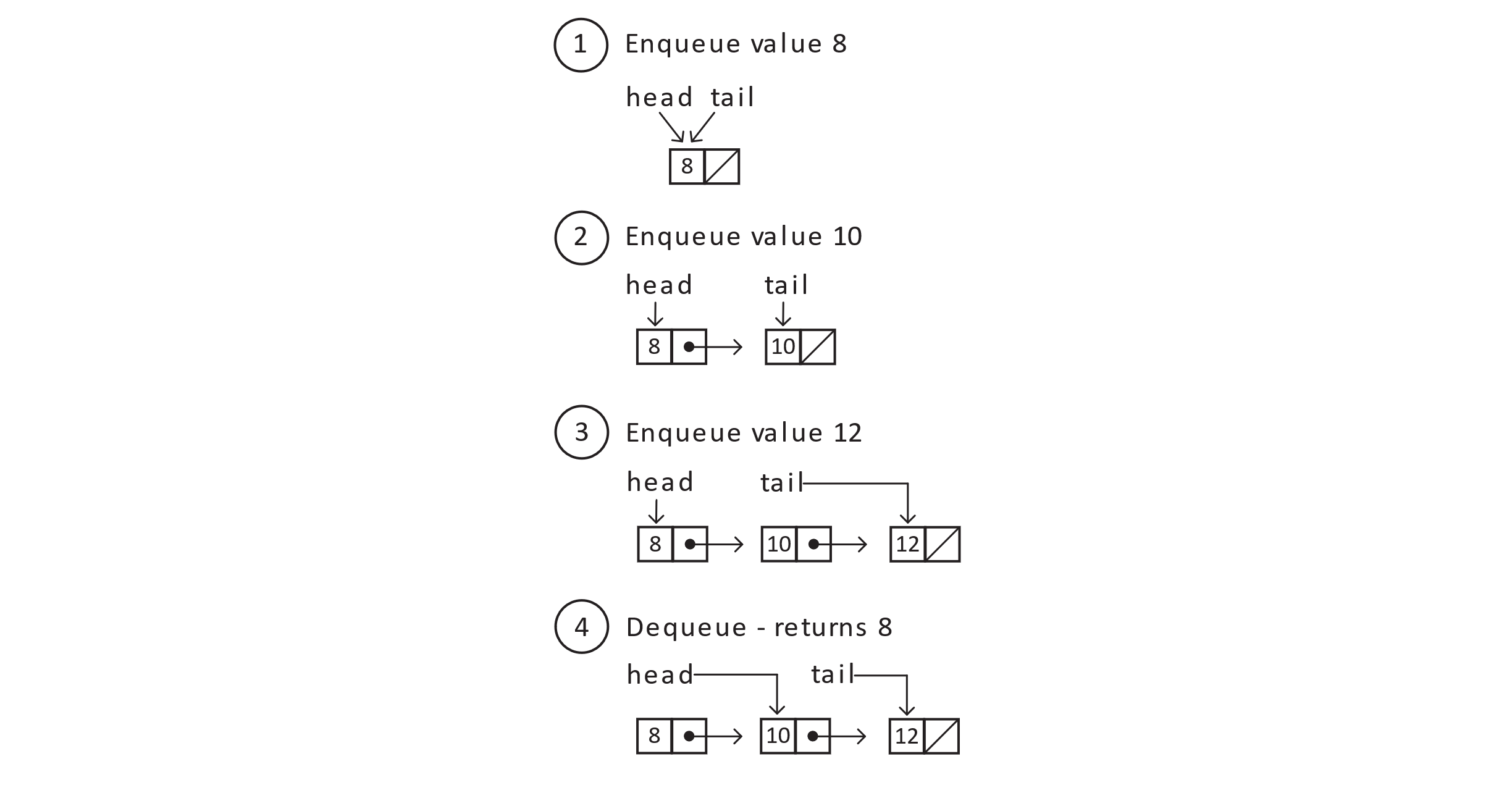
Figure 6.1

First, assess the runtime of each operation. Most operations on linked lists are O(n) due to the fact we have to traverse lists one node reference at a time. In this special case of queues and stacks, no traversal is necessary as long as we maintain a reference to the head or tail. No matter how many elements we enqueue or push, we only ever care about one or two nodes at any given time. The result is an elegant solution that runs in O(1) time for most operations.

Our analysis is not yet complete though, as we must also consider space. Considering that we are working with singly linked nodes, each has a reference and a value. If we want to store 100 integers in our queue or stack, we must have a node for each. Again, assuming that a reference is the same size as an integer, we result in a data structure with twice the overall storage footprint of the data itself. We do, however, still have the slight benefit that it does not have to be stored in contiguous memory locations.

Arrays

Just as we chose to implement a queue and a stack with a linked list, we could likewise choose to store the data in an array. As long as we have definitions for all operations that satisfy the operations specified for the ADT, the result will be just as effective.

Before defining the data structure, we should address the primary challenge when creating array-based queues and stacks. Arrays have a fixed length. Operations on queues and stacks are primarily about adding or removing elements from the underlying structure. How can we use a fixed-length data structure to implement an ADT that necessitates change? The answer typically involves some clever tricks. We define the data structures below and then systematically walk through these tricks:

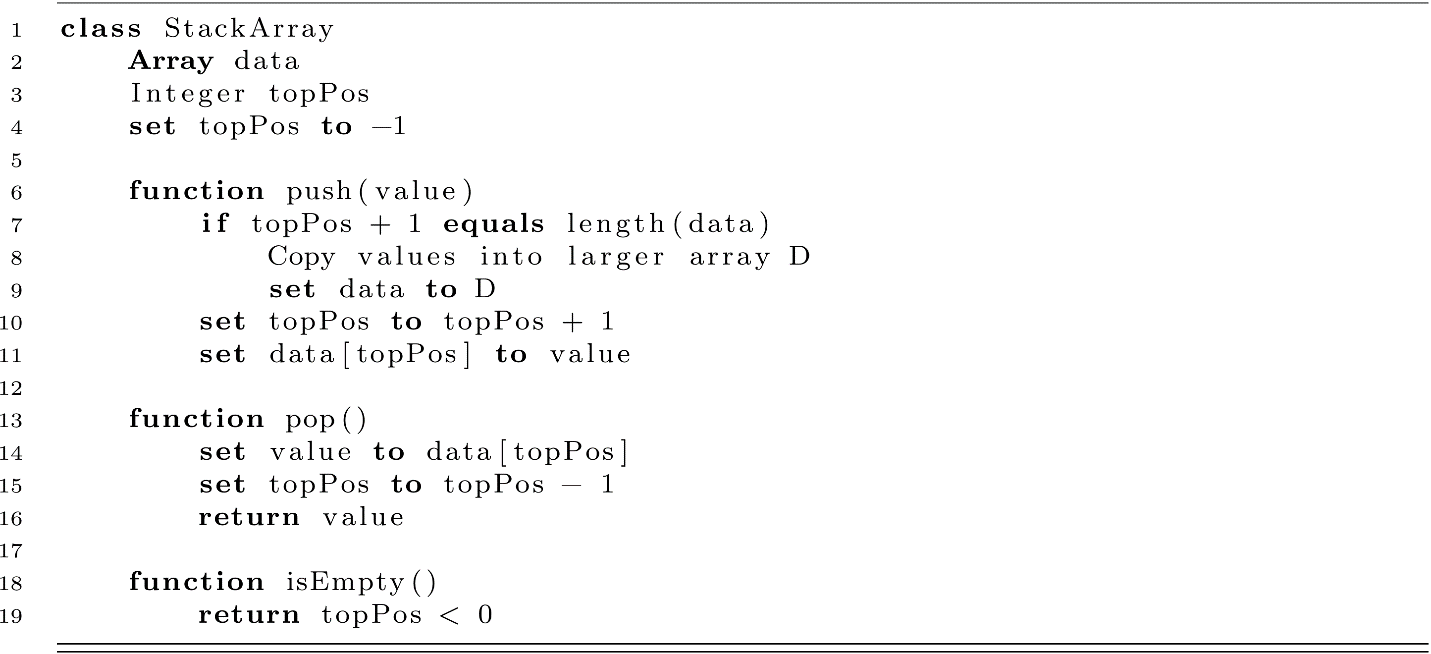
Figure 6.2

Storage Allocation Considerations

How can we ensure we have enough space in our array for the next invocation of enqueue or push? The typical strategy is to initially allocate an array with some amount of excess capacity then reallocate and copy to a larger array as needed. In the QueueArray and StackArray classes, these reallocations occur at lines 11 and 9. This challenge is a balancing act. On one hand, allocating too much space results in waste, as it cannot be used for other purposes while it is part of the allocated array. On the other hand, allocating too little results in more frequent reallocations. This creates issues in two ways.

First, when reallocation is required, our constant-time enqueue or push operation momentarily becomes O(n) with regard to the number of elements stored. From a big-picture perspective, this is not a major issue. Recall from chapter 1 that infrequently required additional steps permit us to talk in terms of amortized cost. The reallocation is indeed expensive but happens so infrequently that other enqueue or push invocations essentially absorb that cost. The result is in an amortized runtime of O(1) for these two operations.

Amortized runtimes do not always tell the same story as nonamortized. In both cases, we can generally expect an invocation to complete efficiently regardless of the number of elements in the queue or stack. The key word here is generally. Consider an application that is responsible for processing a queue with large volumes of real-time data. It may successfully invoke enqueue hundreds of times with a runtime between 5 and 15 milliseconds. A problem arises when the application is dependent on this level of performance because, at some point, an enqueue might trigger a reallocation and instead complete in 500 milliseconds.

The second issue with reallocations pertains to space usage. Not only are we regularly wasting space, but the reallocation itself temporarily consumes excess memory. If we are reallocating and copying from one large array to another, there is a small window of time where the original array and the new array are both consuming precious contiguous blocks of memory. These blocks can be expensive to allocate and even create failures in cases where a large enough contiguous block is not available.

Another clever trick can be applied to queues. Consider what happens when we have an initial array of length 10. We then enqueue and dequeue 10 elements, shifting our head and tail indexes to the end of the array. Our next enqueue will trigger a reallocation even though we are not currently using all 10 spots in our current array. We have the required space allocated but no clear means to access it. The trick lies in how we index into the array. Instead of using tailPos and headPos alone, we still use them but modulo the size of the array. If we do so, our eleventh enqueue and dequeue will use index 10. The result of 10 modulo 10 is 0 and will result in the usage of array position 0. The twelfth enqueue will use index 11, which becomes 1 after modulo 10. Following this strategy (often referred to as wrapping around), we can continue to reuse the original space allocated if our dequeue rate does not lag behind our enqueue rate.

Figure 6.3

Practical Considerations

At the end of the last section, we devised a clever solution to improve the utilization of space already allocated. Although it has improved the data structure on the whole, it now creates a new issue. We now need a new means of determining when to reallocate the array. This can be addressed by keeping an explicit count of how many array elements are currently being used. However, once we have solved that issue, we must then decide how to handle headPos and tailPos. We had relied on using them modulo the size of the array, but now that size has changed. This is the nature of data structures. We often perceive them as static constructs that we study, memorize, and reimplement in new languages. In reality, they are dynamic and evolve as we apply basic concepts to novel problems.

It is also often the case that ADTs and data structures do not exist in isolation. Many languages blend queues and stacks with lists into a single data type. C++ vectors, JavaScript arrays, and Python lists all implement certain operations of these three ADTs (queues, stacks, and lists).

Again, specifying operations in an ADT does not necessarily imply any underlying structure. How, then, do these languages store sequential data? The process typically follows a narrative similar to that of wrapping around in array-based queues. A developer desires some traits of a clever solution, but implementing such a solution then leads to a new set of challenges. Working through these challenges requires both in-depth theoretical knowledge and a grasp of the real-world system. Once considering that real-world context, where modern memory is abundant and constant-time lookups are strongly desirable, most sequential data types make heavier use of arrays than linked lists.