A Boolean Search
Boolean search terms or operators were invented by a mathematician George Boole in 1854. It was quickly forgotten at the time, but it is ideal when applied to searching computerized databases (like a library). Boolean logic uses three operators to demonstrate relationships between terms and definitions. These are AND, OR, NOT. It maybe be helpful to consider the mental model below, to understand how these terms work:
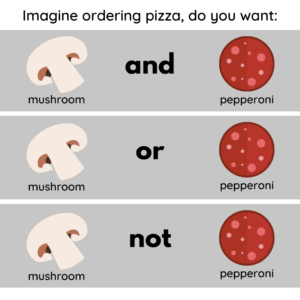
How Boolean Operators Work
Boolean operators aid to narrow the research field. Each operator acts differently with your keywords. Please remember to capitalize the operators in order for them to be recognized by the search engine.
AND
AND means that you wish to connect all of the keywords you have specified in the search bar. AND is most useful when you have many keywords that you are searching for all and all of them should be included in the search results. This will help limit the results, narrowing the amount of research to filter through to determine what is relevant to your needs. But, be careful to not limit your results too far with too many key words. Here’s a example: if you wanted to search for organizational leadership and ethics, it would be beneficial to form your search terms like:
organizational leadership AND ethics
OR
OR is used when you want at least one of the search terms included in the search results. OR guarantees that one of your terms is present, but not necessarily all of the terms. When you use OR, you’ll retrieve more results than if you just searched one of those terms. This is useful when you want to search synonyms or closely related concepts for your topic. Here’s an example, if you wanted to search organizational leadership, but realize that management may also be a relevant alternative to leadership:
organizational leadership OR management
NOT
NOT is used where there are words that may be irrelevant. For example: homonyms. Examples: bat, compacts, desert, fair, lie, hinge, and others. If you repeatedly find results that are matching the wrong definition, using the NOT operator will eliminate some, if not all, of those definitions. For example, consider diversity, equity, and inclusion. Equity has multiple definitions. In this case, you could search for these materials and eliminate unrelated content.
diversity equity inclusion NOT home
Mixing Operators
Once you understand how Boolean operators work you can begin to mix them together to filter results more thoroughly. First, you can combine OR and AND. Here’s an example that combines some of the previous examples, recognizing that leadership and management may be synonymous, but you would also like a connection to ethics. This is just an example of how two operators can work together, you can also combine NOT with another operator.
(organizational leadership OR management) AND ethics.
The ultimate example is to combine all of the operators. Remember that you may have to test searching with different terms and operators in order to find the right results for your research. Sometimes adding a second or third operator, may restrict the results too much or not in the way you intended. Here’s an example to consider that combines all three operators.
(organizational leadership OR management) AND equity NOT home
Conclusion:
To conclude, try searching in Google or another search engine to test out the Boolean operators. This is a helpful strategy to use when researching content. The following resources may be additional, helpful resources that can further your education related to Boolean searching.
More resources related to Boolean searching
- Search Logic and Boolean Connectors, University of Minnesota
- Boolean Operators, Iowa State University
- How to Conduct a Boolean Search, Coalition of Essential Schools
References for Remixed Content:
EMU Library (2019, April 1). Research tip: An introduction to Boolean searching [Video]. YouTube. https://www.youtube.com/watch?v=qYGAaiwX3VA
Hanson, K. & Paul, P. (n.d.). Information strategies for communicators. University of Minnesota. Retrieved May 25, 2022, from https://open.lib.umn.edu/infostrategies/chapter/8-9-search-logic-and-boolean-connectors/
Quibell, A. & Cramer, E. (n.d.) 6.8 Boolean operators. eCampus Ontario. Retrieved May 25, 2022, from https://ecampusontario.pressbooks.pub/gccomm/chapter/boolean-operators/

